X Lines

Lines

Lines are defined by linear equations with two variables ($y = 3x + 2$). One can plug in values to probe for a solution:
$(1,5)$ -> $5 = 5$ is true and therefore a point on the line.
$(-2,-3)$ -> $-3 = -4$ is false and therefore not a point on the line.

When talking about graphs the parantheses around a set of values denote a point.

For lines we only need two points (solutions) to find all the points on them.

Given a line equation there are two methods to find two points on the line (allowing one to graph it).

Standard form (intercept method)

The equation needs to be in standard form, with x and y on one side and the constant term on the other side: $2x + 3y = 6$. Since we know that the x-intercept has a y value of 0, and the y-intercept has an x value of 0, plugging these numbers in allows us to solve for the x and y values of the intercepts respectively. In this case (3,0) and (0,2).

This method does not work when the constant of the equation is 0, because attempting to solve using this method on such an equation would always result in two points (0,0).

If the equation contains fractions it can be solved for y to prepare for the slope-intercept method (this eliminates the need for finding the LCD to get rid of the fractions). Example:

$-\frac 3 4 x + \frac 1 2 y = \frac 1 2$ | $+\frac 3 4 x$
$\frac 1 2 y = \frac 3 4 x + \frac 1 2$ | $\times 2$
$y = \frac 6 4 x + 1$
$y = \frac 3 2 x + 1$

Slope-intercept form

The equation needs to be solved for y for this method to work. Assuming the following equation
$y = 3x + 2$
The constant 2 is always the y-coordinate of the y-intercept (the point where the line crosses the y axis, which has an x value of 0). This reveals that (0,2) is a point on the line of the above equation.
The coefficient of x is the slope of the line. When read as a fraction (in this case $\frac 3 1$ the numerator describes how much to move up or down while the denominator describes how far to move to the right in order to find another point. Therefore (1,5) can be identified to be another point on the same line.

This method can be easier to work with if the intercept method yields only fractions.

Horizontal and Vertical Lines

Are defined by linear equations with only one variable.

$2x = 8$
$x = 4$ -> a straight, vertical line that crosses the x axis at 4. For any given value of y, the value of x is always 4.

$-3y = 9$
$y = -3$ -> a straight, horizontal line taht crosses the y axis at -3. For any given value of x, the value of y is always -3.

Slopes

The slope of a line is defined as a ratio of its rise over its run $m = \frac {RISE} {RUN}$.

Slope Formula

Given the two points $(x$1, y1) and $(x$2, y2):
$m = \frac {y$2 - y1} {x2 - x1}

Rise: How much the line moves up or down from any given point. Can be positive (rising line) or negative (falling line). Run: How much the line moves to the right from any given point. Is always positive (from left to right).

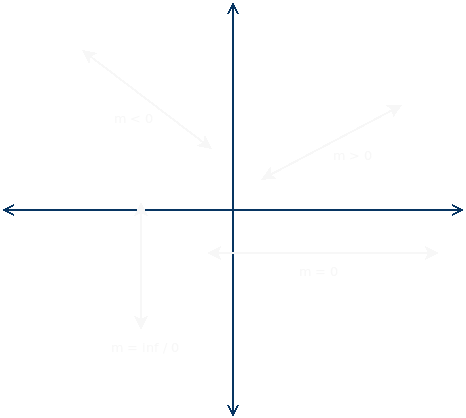
Given the above formula a line's slope can be found given any two of its points. The slope then can be used to find the line's equation.

Point-slope Formula

The slope-intercept from of a line's equation can be derived if only the slope and one point on it are known. Assuming a line's slope is $3$ and one of its points is $(1,2)$, its slope formula would appear as
$3 = \frac {y-2} {x-1}$ which can be solved into the point-slope formula by multiplying by the right hand's denominator, leaving us with
$y-2 = 3(x-1)$ -> $y = 3x - 1$

Parallel and Perpendicular Lines

Two lines that never touch each other at any point are parallel to each other. They have the same orientation (slope).
When one line crosses another at a right angle it is perpendicular to that line.

Parallel lines share the same slope -> $m$1 = m2
The slope of a line perpendicular to another line is the opposite reciprocal of that line -> $m$1 = \frac 7 5, m2 = \frac {-5} {7}