Trigonometry Basics (Tangent, Sine, Cosine Functions)

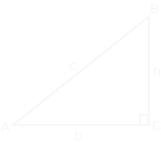
Each angle of a right-angled triangle has a constant ratio called the tangent.

Angle Notation

$\text{ABC} \Rarr$ The angle at point $B$.
$\text{BAC} \Rarr$ The angle at point $A$.

Or just $\angle B$, $\hat{B}$ or $\angle A$, $\hat{A}$

Lowercase greek letters are also commonly used to denote angles:

Tangent Function

The tangent function of an angle is equal to the ratio of the angle's opposite and adjacent sides.

Given $\theta\degree = BAC$ and $\phi\degree = ABC$

Applicable angles are either of the two angles that are not $90\degree$.

So

$\tan \theta\degree = \frac h b$
$\tan \phi\degree = \frac b h$

Inverse Tangent Function

The tangent function's inverse calculates an angle based on a known ratio.

$\tan^{-1} \frac h b = \theta\degree$

Facts

All angles of a right-angled triangle always sum up to $180\degree$. Since the right-angle is always one of $90\degree$, the remaining angles always add up to another $90\degree$. Therefore:

$90\degree - \theta\degree = \phi\degree$ and
$90\degree - \phi\degree = \theta\degree$

$\tan 45\degree = 1$
$\tan 90\degree = \text{invalid}$

The angle being worked on is called the angle of focus. That angle's tangent ratio is always $\frac{\text{opposite}}{\text{adjacent}}$

Sine and Cosine Functions

$\sin \theta\degree = \frac{\text{opposite}}{\text{hypotenuse}}$
$\cos \theta\degree = \frac{\text{adjacent}}{\text{hypotenuse}}$

The inverse functions $\sin^{-1}$ and $\cos^{-1}$ yield the angle given a ratio.

Non-right-angled Triangles

Any angle with a perpendicular opposite can be found by bisecting the opposite at that angle by creating two right-angled triangles.

Pythagorean Identity and Theorem

$\cos^2\theta + \sin^2\theta = 1$

$a^2 + b^2 = c^2$ where $a$ and $b$ are equal to the lengths of the adjacent and opposite, and $c$ is equal to the length of the hypotenuse.

Relationship of the Functions

Since $\sin \theta\degree = y$, and $\cos \theta\degree = x$, and
$\tan \theta\degree = \frac y x$, it follows that:

$\tan \theta\degree = \frac {\sin \theta\degree}{\cos \theta\degree}$